스포일러를 피하기 위해 후기 글과 분리했습니다. 이 글에서는 저희 팀이 푼 문제들의 풀이와, 풀이에 도달하기까지의 과정을 다룹니다. 대회의 자세한 후기에 대해서는 UCPC 2020 후기 글을 참조해 주세요.
예선
해결한 문제: A, C, D, G, H, I, J (7문제 해결, 25위)
풀이는 해결한 시간 순서대로 작성했다.
원이가 연립방정식의 해 공식을 그대로 코딩해서 해결했다.
재혁이가 풀었다. 나무 높이 합은 3의 배수여야 하고, 1만큼 성장시키는 물뿌리개가 2만큼 성장시키는 물뿌리개보다 많이 필요하면 안 된다.
팀원들은 각자 일정이 있어서 이 문제부터는 내가 풀었다. ㅈ 그래프를 세는 법은 원이가 아이디어를 냈는데, 중심이 되는 노드를 잡고 연결된 간선 세 개를 고르는 경우의 수를 세어 주면 된다. ㄷ 그래프도 비슷하게 중심이 되는 간선을 잡으면 되는데, 그걸 못 떠올려서 트리 DP로 길이 1–3짜리 경로의 수를 세었다. 참고로 문제 제목은 "두둥 등장"이라고 읽는다.
BFS를 돌리는데, 이웃한 노드를 곧장 큐에 넣는 대신 그 노드를 발견한 횟수가 degree의 절반 이상이 되는 순간 큐에 넣어준다. BFS를 이런 식으로 변형한 문제는 처음 봐서 재밌었다.
알고리즘 지식보다는 논리력을 요구하는 문제다. 예선 문제 중 가장 마음에 드는 문제였다.
우선 문제의 조건을 다음과 같이 해석할 수 있다.
"모임이 끝난 뒤 참가자 중 감염되지 않은 사람이 있다면, 모임에 참여한 모든 사람은 감염된 적이 없다."
따라서 어느 시점의 비감염자 목록을 안다면 그 이전 시점의 비감염자 목록도 알아낼 수 있다. 모임을 시간 역순으로 훑어서 초기 비감염이 확실한 사람들을 골라낸다. 이제 남은 사람들의 감염 여부를 판별하는 일이 남았다. 이 사람들을 감염자 후보라고 부르자.
감염자 후보들을 전부 감염시키고 모임을 시뮬레이션했을 때, 최종 감염자 목록과 동일하게 나온다면 원하는 답을 찾은 것이다. 반면 최종 감염자 목록과 동일하지 않게 나왔다고 가정하면 다음 두 가지 가능성이 있다.
- 최종 비감염자인 사람이 시뮬레이션 결과 감염자가 된 경우: 이 사람이 참여한 모임 중 감염자가 참가한 모임이 있다는 뜻인데, 초기 비감염자를 찾는 과정에서 그런 경우를 모두 걸러냈으므로 모순이다.
- 최종 감염자인 사람이 시뮬레이션 결과 비감염자가 된 경우: 이 사람을 감염시키려면 다른 초기 감염자가 더 필요한데, 이미 모든 후보를 초기 감염시킨 상태이므로 이 사람을 감염시키는 게 불가능하다.
따라서 시뮬레이션 결과와 최종 감염자 목록이 다르면 답이 존재하지 않는다.
온갖 시도 끝에 성공해서 기분이 좋았던 문제다. 처음에는 비트 필드를 이용해서 효율적으로 브루트 포싱을 해야 하는 문제라고 생각했다. 우선 수식을 AST (Abstract Syntax Tree)로 파싱한 뒤 나이브하게 모든 경우를 계산하는 코드를 짰다. 예상한 대로 시간 초과가 났다.
그래서 다음과 같이 최적화하는 방법을 떠올렸다. AST 노드의 계산값은 서브트리에 포함된 변수의 값이 바뀌지 않는 이상 일정하게 유지되므로, 계산값을 캐싱하는 것이 가능하다. 캐싱이 효율적이려면 브루트 포싱을 할 때 변수값 변경을 최소화해야 한다. 그레이 코드를 이용해서 매번 변수값을 하나씩만 바꿔 준다면 노드를 재계산하는 일이 최소가 될 것이다. 그럴듯한 풀이라는 생각이 들어서 열심히 구현해 제출했고 결과는... 여전히 시간 초과였다. 아무래도 모든 경우를 돌아보는 시간 자체가 오래 걸리는 것 같았다.
다른 최적화 방법을 고민하다가 이런 관찰을 했다. 식에서 사용하지 않는 변수가 있는데도 그 변수까지 변경하면서 브루트 포싱을 하는 것은 비효율적이다. 사용한 변수를 관리하고, 그 변수들만 브루트 포싱하면 되지 않을까? 물론 주어진 식이 a부터 z까지 모든 변수를 사용하면 문제가 되겠지만 AST의 서브트리 중에서는 일부 변수만 사용하는 트리도 많을 것이다.
위 관찰을 통해 떠올린 풀이는 다음과 같다. 처음에 모든 변수를 미정 상태로 두고, 트리를 내려가면서 조건문에 등장한 변수들의 값을 0이나 1로 지정해 준다. 조건문의 계산값에 따라 노드의 왼쪽 자식으로 내려가야 하는지 오른쪽 자식으로 내려가야 하는지가 정해진다. 리프 노드의 변수까지 정해주고 나면 k = (미정 상태인 변수 개수)를 센다. 미정 상태인 변수들을 무엇으로 정해 주든 계산값이 변하지 않으므로 경우의 수는 2^k 가지일 것이다. 이런 식으로 백트래킹하면서 조건문의 변수들을 가능한 모든 조합으로 지정해 주고, 리프 노드의 계산값이 0인 경우의 수를 전부 더하면 답이 된다. 이렇게 하니 실행 시간 0ms가 나왔다.
내 풀이는 출제진 풀이와 다른데, 출제진 풀이의 발상도 재미있었다. 숏코딩 문제가 비슷한 테크닉을 사용한다고 하니 나중에 한 번 풀어봐야겠다.
우선 이 문제를 풀기 위해 꽉 채운 노트 두 페이지를 감상하자.
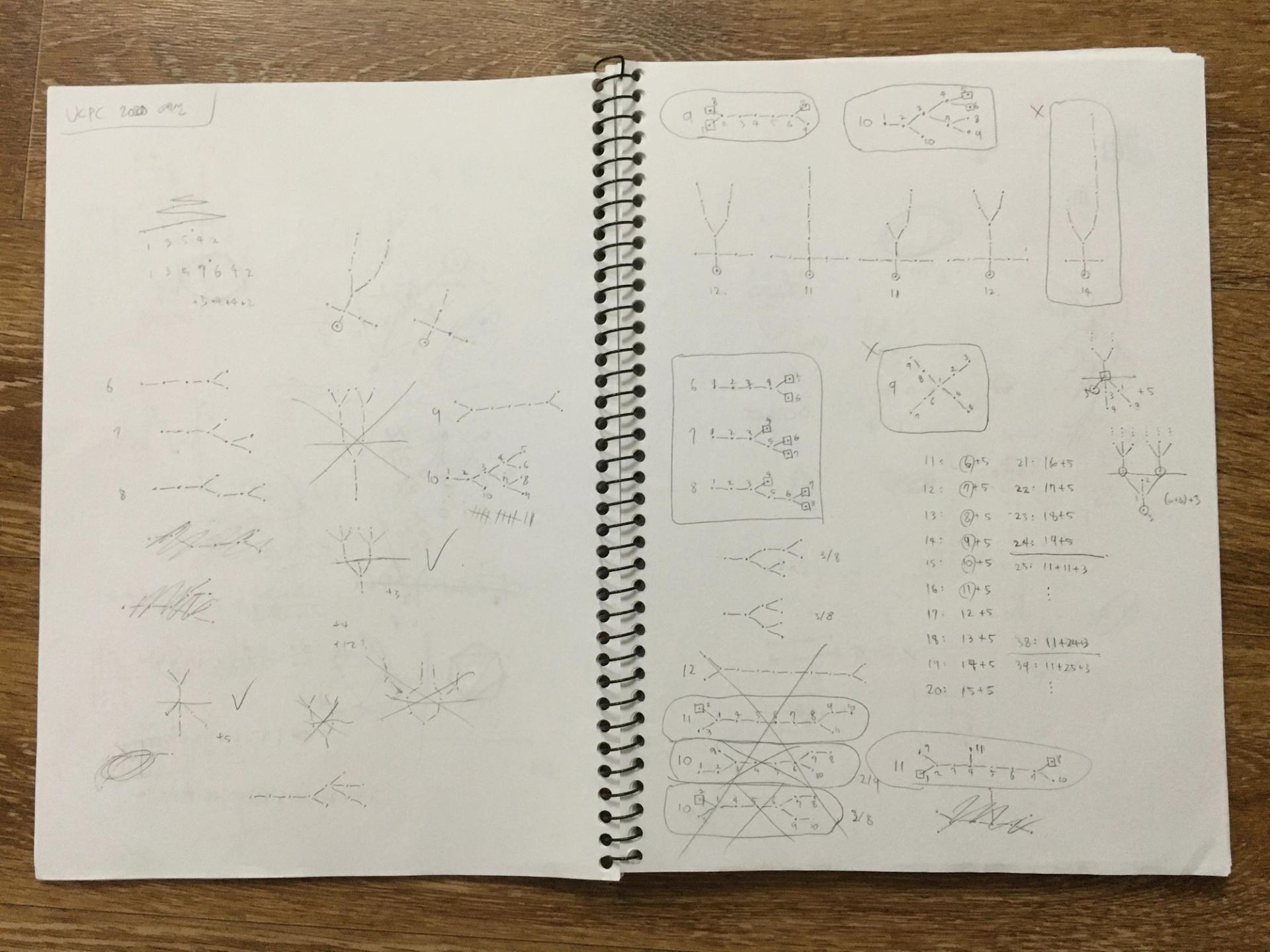
새벽 1시 반쯤 E번 감자 농장을 고민하다가 재혁이가 I번 문제를 시도하고 있길래 함께 봤고, 그럴듯한 접근을 떠올렸다. 두 ㄷㄷㄷㅈ 트리를 하나로 엮어 새로운 ㄷㄷㄷㅈ 트리를 만드는 방법을 찾은 뒤, 분할 정복 하듯 트리를 구성하는 것이다. 풀이에 도달하기까지 사고의 흐름을 대강 정리해 봤다.
- 무엇부터 시작해야 할지 몰라서 우선 크기 6, 7, 8짜리 ㄷㄷㄷㅈ 트리를 손으로 직접 찾아줬다.
- 한참 이것저것을 그려보다가 두 ㄷㄷㄷㅈ 트리에 노드 세 개를 추가해서 엮는 방법을 찾는 데 성공했다. 추가하는 노드 세 개와 간선들을 결합 모듈, 엮을 두 트리를 부품이라고 부르자. 아쉽게도 부품이 특정 조건을 만족해야 했기 때문에 위에서 찾은 ㄷㄷㄷㅈ 트리들을 부품으로 사용할 수는 없었다. 결합 모듈은 부품의 조건을 만족하도록 찾아주었다. 그래야 결합한 트리를 다시 부품으로 쓸 수 있기 때문이다.
- 부품을 손으로 찾아보기 시작했다. 크기 11, 12, 14짜리 부품을 찾았다. 아마 11이 부품의 최소 크기인 것 같다. 크기 13인 부품은 찾는 데 실패했다.
- 이번에는 두 트리가 아니라 하나의 트리에 붙일 모듈을 생각해 봤다. 한참 실험하다가 트리에 노드 5개를 붙여 새로운 ㄷㄷㄷㅈ 트리를 만드는 방법을 찾아냈다.
- 우연의 일치로 붙일 노드 5개의 모양이 부품의 조건을 만족했다. 이 노드 5개를 변환 모듈, 기존 트리를 재료라고 부르자.
- 더 놀라운 것은, 재료의 조건은 만족하기 쉬웠다는 점이다. 앞서 찾은 크기 6, 7, 8짜리 트리도 변환 모듈을 붙일 수 있는 곳이 여러 군데 있었다. 이제 재료들만 잘 찾아주면 여기에 변환 모듈을 덕지덕지 붙여 원하는 크기의 부품을 만들 수 있다! 속으로 환호성을 질렀다.
- 손으로 직접 크기 6, 7, 8, 9, 10, 11짜리 재료들을 찾아줬다. 이제 남은 건 코딩이다. 재료에 변환 모듈을 붙여 크기 11–24의 부품들을 만들었다. N≥25인 트리는 크기 11 부품과 크기 N-14 부품을 결합 모듈로 붙여 주었다.
문제를 풀고 나니 새벽 4시가 되었다. 피곤했지만 기분 좋게 잠들었다.
대회가 끝나고 종서(leejseo)의 풀이를 들었다. 고등학교 후배이자 친구이고, 이번 UCPC 참가자이다. 종서는 트리에 크기 8짜리 모듈을 반복적으로 붙이는 방식으로 풀었다. 듣고 보니 내 풀이도 사실상 크기 14짜리 모듈을 반복적으로 붙이는 풀이였는데, 분할 정복에 생각이 갇혀서 복잡하게 접근한 것 같다. (참고로 크기 5인 변환 모듈을 반복적으로 붙이는 건 불가능한데, 재료에 변환 모듈을 붙일 때마다 붙일 수 있는 곳이 하나씩 줄어들기 때문이다.)
비록 C, I번 문제를 비효율적으로 접근했지만 의미 없는 접근은 아니었다고 생각한다. 풀이를 찾는 과정에서 새로운 가능성을 익혔고, 시야를 넓힐 수 있는 좋은 경험이었다.
본선
해결한 문제: A, C, L (3문제 해결, 89위)
높이가 D 이상인 노드만 방문하면 되니, DFS를 통해 각 노드의 높이를 구하고 방문할 노드 개수를 센다. 최소한으로 이동하려면 방문할 노드를 잇는 간선들을 한 번씩 왕복하면 되므로, 방문할 노드 개수에서 1을 빼고 2를 곱하면 답이 된다. 루트의 높이가 D보다 작은 엣지 케이스에 주의하자.
원이가 전날 연습 때 HLD를 써서 문제를 푼 기억이 강렬하게 남았는지 HLD로 풀었다고 한다. 분해한 경로 길이에서 D를 빼고, 이 중 음이 아닌 값들을 더해서 왕복할 간선의 개수를 센 것 같다. 올해는 shortest code 특별상이 있었는데, 대신 longest code 특별상이었다면 조금 기대를 할 수 있었을지도 모르겠다(?)
처음에는 SCC로 접근했는데 SCC를 사용하는 문제를 많이 안 풀어봐서 코딩하는 데 오래 걸렸고 답도 틀렸다. 스코어보드를 보니 C와 L이 A 다음으로 많이 풀린 문제길래, 현재의 복잡한 풀이를 디버깅하는 것보다 간단한 풀이를 찾는 것이 빠를 거라고 생각했다. 그렇게 새로 찾은 풀이는 다음과 같다.
우선 함수 그래프 노드의 종류는 두 가지가 있다. 사이클에 포함되어 있는 것과, 그렇지 않은 것이다. 후자를 편의상 꼬리라고 부르자. 꼬리를 따라가다 보면 사이클에 도달하게 된다.
운영진 풀이에서는 사이클에 포함된 점부터 찾아냈는데, 나는 사이클을 찾는 방법을 떠올리지 못해서 꼬리부터 찾았다. 다른 노드로부터 도달할 수 없는 노드는 꼬리이다. (주의: 다른 노드에도 도달할 수 없는 노드는 예외적으로 꼬리가 아니다. 자기 자신으로 가는 사이클에 포함되는 노드이기 때문이다.) 그런 꼬리를 하나씩 제거하면서, 꼬리가 향할 수 있는 노드의 수를 답에 곱해준다. 결국 남는 노드는 사이클에 포함된 노드밖에 없을 것이다.
각 사이클에 대해 가능한 함수의 가짓수는 (사이클 크기 - 1)! 이다. 원순열을 생각하면 이해하기 쉽다. 이제 이것들을 마저 답에 곱해 주면 된다.
어려웠던 부분은 꼬리가 향할 수 있는 노드를 찾는 것이었다. 답부터 말하자면 도달 가능한 노드 중 "도달할 수 있는 다른 노드가 가장 많은 노드"이다. 다른 말로 하면, 도달 가능성 그래프에서 outdegree가 가장 큰 노드이다. 만약 outdegree가 더 적은 노드를 향했다면, 그 노드에서 outdegree가 더 많은 노드에 도달할 수 있다는 사실에 모순이기 때문이다. outdegree가 가장 많은 노드가 여러 개라면 이 노드들은 사이클을 이루는 것이고, 이들 중 어느 쪽을 향해도 된다.
SCC를 사용하지 않는 풀이로 풀면서도 어려운 문제라고 생각했는데, 대회에서는 어떻게 이렇게 많이 풀린 걸까? 훨씬 쉬운 접근 방법이 있을지도 모르겠다.
DP라는 건 바로 떠올렸지만, 처음에 접근 방향을 잘못 잡아서 한참 헤맸던 문제다. 대회 종료 30분 전이 되어서야 올바른 DP 식을 떠올릴 수 있었다.
특정 구간의 피자가 남았을 때, 양 끝 피자 중 어떤 것을 먹어야 최종적인 상대와의 점수차를 최대화할 수 있는지 보면 된다. 어떤 것을 먹을지 결정하기 위해서는 현재 상대와의 시간차도 고려해야 한다. 피자를 먹고도 여전히 시간이 상대보다 앞서서 이득을 볼 수도 있고, 너무 큰 피자를 먹어서 상대에게 턴이 넘어가 손해를 볼 수도 있기 때문이다. DP 테이블은 다음과 같이 정의한다.
D[i][j][k] : i–j 구간의 피자가 남았고 내가 k+0.5초 앞서는 상황일 때, 남은 피자를 마저 먹고 나서 (나의 점수)-(상대 점수)를 최대화한 값
여기서 구간은 양 끝이 이어져 있다고 생각한다. 예컨대 4–2 구간이라고 하면 4번 이후의 모든 피자와 1, 2번 피자들로 이루어진 구간이 된다.
주의할 점은 "현재까지의 점수차"를 최대화하는 게 아니라 "앞으로의 점수차"를 최대화해야 한다는 점이다. 게임에서 중요한 것은 중간 점수가 아니라 최종 점수이기 때문이다. 처음 접근에서는 현재까지의 점수를 저장하는, 또 피자를 구간의 안쪽부터 먹게 되는 이상한 DP 식을 짰고 예제조차 답이 나오지 않아서 헤맨 것이었다.
DP 테이블의 계산값이 가질 수 있는 가능성은 크게 두 가지가 있다. 일반성을 잃지 않고 구간의 왼쪽 (i번째) 피자를 먹는 게 최적이라고 하자.
- 왼쪽 피자를 먹고, 내가 여전히 상대보다 앞선 경우: i번째 피자의 크기를
p[i]라고 하면, 피자를 먹고 나서 상대와의 시간차는k-p[i](+0.5초)가 된다. DP 값은 피자의 점수p[i]에다D[i+1][j][k-p[i]]을 더한 값이 된다. (모듈로 연산은 생략한다.) - 왼쪽 피자를 먹고, 내가 상대보다 뒤처지게 된 경우: 피자를 먹고 나면 상대는 나보다
p[i]-k-1(+0.5초)만큼 앞서게 된다. 이번에는 상대가 자신의 점수를 최대화하려고 할 것이므로, DP 값은p[i]에서 상대가 최대화한 점수차인D[i+1][j][p[i]-k-1]를 뺀 값이 된다.
오른쪽 피자를 먹는 게 최적인 가능성도 따져서 둘 중 최댓값을 DP 값으로 정해 준다. 이제 모든 i에 대해 D[i][i-1][0] 중 최대인 값을 구하면 전체 게임에서의 최대 점수차를 구할 수 있다. 점수의 총합 (실버+브론즈)와 최대 점수차 (실버-브론즈)를 더해 2로 나눠 주면 실버가 최대로 먹을 수 있는 피자의 양이 된다.
B와 D는 본선 때 시간이 부족해서 건드리지 못했지만, 본선이 끝나고 개인적으로 풀어본 문제이므로 풀이를 짤막하게 설명해 둔다.
몇 가지 경우를 직접 생각해 보면, 각 행에서 시작 방의 위치가 항상 연속해서 나타나야 함을 알 수 있다. 행을 하나씩 훑으면서 이 구간을 투 포인터로 관리해 주고, 구간들의 길이 합을 구하면 된다.
헛간의 거리들의 합을 생각하는 대신, "각 항로를 지나는 헛간 쌍의 수"를 세어 항로 길이와 곱해 모두 더한 값을 생각할 수 있다.
항로를 지나는 헛간 쌍의 수는, 항로의 한쪽 끝에 연결된 헛간의 수와 반대쪽 끝에 연결된 헛간의 수를 곱한 값이다. 항로가 i번째 헛간과 j번째 헛간을 잇는다고 하면, 헛간 쌍의 수는 이웃한 항로들을 어떻게 잇는지에 따라 1*(M+N-1) 또는 (i+j-1)*(M+N-i-j+1) 중 하나가 된다.
DP 값을 "위쪽의 1~i번째 헛간들과 아래쪽의 1~j번째 헛간들을 모두 이었을 때 최소의 비용"이라고 정의하자. 여기서 비용이라 함은, "항로를 지나는 헛간 쌍의 수"를 미리 계산해서 거리와 곱해 더한 값이다. 이는 마지막 두 항로가 새로 추가할 항로와 같은 헛간을 공유할지 아닐지에 따라 달라지므로, DP 테이블에 "마지막 두 항로가 어느 헛간 (위 또는 아래)를 공유하는지"에 대한 정보도 저장해 준다.
DP 식을 계산할 때 마지막으로 추가한 항로는 아직 "항로를 지나는 헛간 쌍의 수"가 정해지지 않은 상태이므로 DP 값은 (i, j) 항로의 비용을 포함하지 않아야 한다. (N, M)번째 DP 값에다 (N, M) 항로의 비용까지 더해 주면 답이 된다.